Using Variational Estimates to Initialize the NUTS-HMC Sampler¶
In this example we show how to use the parameter estimates return by Stan’s variational inference algorithm as the initial parameter values for Stan’s NUTS-HMC sampler. By default, the sampler algorithm randomly initializes all model parameters in the range uniform[-2, 2]. When the true parameter value is outside of this range, starting from the ADVI estimates will speed up and improve adaptation.
Model and data¶
The Stan model and data are taken from the posteriordb package.
We use the blr model, a Bayesian standard linear regression model with noninformative priors, and its corresponding simulated dataset sblri.json, which was simulated via script sblr.R. For
conveince, we have copied the posteriordb model and data to this directory, in files blr.stan and sblri.json.
[1]:
import os
from cmdstanpy import CmdStanModel
stan_file = 'blr.stan' # basic linear regression
data_file = 'sblri.json' # simulated data
model = CmdStanModel(stan_file=stan_file)
print(model.code())
INFO:cmdstanpy:compiling stan file /home/docs/checkouts/readthedocs.org/user_builds/cmdstanpy/checkouts/v1.0.0rc3/docsrc/examples/blr.stan to exe file /home/docs/checkouts/readthedocs.org/user_builds/cmdstanpy/checkouts/v1.0.0rc3/docsrc/examples/blr
INFO:cmdstanpy:compiled model executable: /home/docs/checkouts/readthedocs.org/user_builds/cmdstanpy/checkouts/v1.0.0rc3/docsrc/examples/blr
data {
int <lower=0> N;
int <lower=0> D;
matrix [N, D] X;
vector [N] y;
}
parameters {
vector [D] beta;
real <lower=0> sigma;
}
model {
// prior
target += normal_lpdf(beta | 0, 10);
target += normal_lpdf(sigma | 0, 10);
// likelihood
target += normal_lpdf(y | X * beta, sigma);
}
Run Stan’s variational inference algorithm, obtain fitted estimates¶
The CmdStanModel method variational runs CmdStan’s ADVI algorithm. Because this algorithm is unstable and may fail to converge, we run it with argument require_converged set to False. We also specify a seed, to avoid instabilities as well as for reproducibility.
[2]:
vb_fit = model.variational(data=data_file, require_converged=False, seed=123)
INFO:cmdstanpy:Chain [1] start processing
INFO:cmdstanpy:Chain [1] done processing
WARNING:cmdstanpy:The algorithm may not have converged.
Proceeding because require_converged is set to False
The ADVI algorithm provides estimates of all model parameters.
The variational method returns a CmdStanVB object, with method stan_variables, which returns the approximate estimates of all model parameters as a Python dictionary.
[3]:
print(vb_fit.stan_variables())
{'beta': array([0.997115, 0.993865, 0.991472, 0.993601, 1.0095 ]), 'sigma': 1.67}
Posteriordb provides reference posteriors for all models. For the blr model, conditioned on the dataset sblri.json, the reference posteriors are in file sblri-blr.json
The reference posteriors for all elements of beta and sigma are all very close to 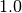 .
.
The experiments reported in the paper Pathfinder: Parallel quasi-Newton variational inference by Zhang et al. show that mean-field ADVI provides a better estimate of the posterior, as measured by the 1-Wasserstein distance to the reference posterior, than 75 iterations of the warmup Phase I algorithm used by the NUTS-HMC sampler, furthermore, ADVI is more computationally efficient, requiring fewer evaluations of the log density and gradient functions. Therefore, using the estimates from ADVI to initialize the parameter values for the NUTS-HMC sampler will allow the sampler to do a better job of adapting the stepsize and metric during warmup, resulting in better performance and estimation.
[4]:
vb_vars = vb_fit.stan_variables()
mcmc_vb_inits_fit = model.sample(
data=data_file, inits=vb_vars, iter_warmup=75, seed=12345
)
INFO:cmdstanpy:CmdStan start procesing
INFO:cmdstanpy:CmdStan done processing.
[5]:
mcmc_vb_inits_fit.summary()
[5]:
| Mean | MCSE | StdDev | 5% | 50% | 95% | N_Eff | N_Eff/s | R_hat | |
|---|---|---|---|---|---|---|---|---|---|
| name | |||||||||
| lp__ | -160.00 | 0.054000 | 1.80000 | -160.00 | -160.00 | -150.00 | 1100.00 | 1000.00 | 1.00 |
| beta[1] | 1.00 | 0.000013 | 0.00097 | 1.00 | 1.00 | 1.00 | 5613.00 | 5270.00 | 1.00 |
| beta[2] | 1.00 | 0.000017 | 0.00120 | 1.00 | 1.00 | 1.00 | 4801.00 | 4508.00 | 1.00 |
| beta[3] | 1.00 | 0.000013 | 0.00093 | 1.00 | 1.00 | 1.00 | 5377.00 | 5049.00 | 1.00 |
| beta[4] | 1.00 | 0.000015 | 0.00110 | 1.00 | 1.00 | 1.00 | 4875.00 | 4578.00 | 1.00 |
| beta[5] | 1.00 | 0.000014 | 0.00100 | 1.00 | 1.00 | 1.00 | 5573.00 | 5233.00 | 1.00 |
| sigma | 0.96 | 0.000000 | 0.07000 | 0.86 | 0.96 | 1.09 | 270.85 | 254.32 | 1.01 |
The sampler estimates match the reference posterior.
[6]:
print(mcmc_vb_inits_fit.diagnose())
Processing csv files: /tmp/tmpz1qbkg8k/blr-20211119014526_1.csv, /tmp/tmpz1qbkg8k/blr-20211119014526_2.csv, /tmp/tmpz1qbkg8k/blr-20211119014526_3.csv, /tmp/tmpz1qbkg8k/blr-20211119014526_4.csv
Checking sampler transitions treedepth.
Treedepth satisfactory for all transitions.
Checking sampler transitions for divergences.
No divergent transitions found.
Checking E-BFMI - sampler transitions HMC potential energy.
E-BFMI satisfactory.
Effective sample size satisfactory.
Split R-hat values satisfactory all parameters.
Processing complete, no problems detected.
Using the default random parameter initializations, we need to run more warmup iteratons. If we only run 75 warmup iterations with random inits, the result fails to estimate sigma correctly. It is necessary to run the model with at least 150 warmup iterations to produce a good set of estimates.
[7]:
mcmc_random_inits_fit = model.sample(data=data_file, iter_warmup=75, seed=12345)
INFO:cmdstanpy:CmdStan start procesing
INFO:cmdstanpy:CmdStan done processing.
[8]:
mcmc_random_inits_fit.summary()
[8]:
| Mean | MCSE | StdDev | 5% | 50% | 95% | N_Eff | N_Eff/s | R_hat | |
|---|---|---|---|---|---|---|---|---|---|
| name | |||||||||
| lp__ | -190.0 | 25.00000 | 36.0000 | -230.00 | -170.0 | -160.0 | 2.0 | 4.8 | 13.0 |
| beta[1] | 1.0 | 0.00012 | 0.0021 | 1.00 | 1.0 | 1.0 | 293.0 | 698.0 | 1.0 |
| beta[2] | 1.0 | 0.00020 | 0.0029 | 0.99 | 1.0 | 1.0 | 204.0 | 485.0 | 1.0 |
| beta[3] | 1.0 | 0.00013 | 0.0021 | 1.00 | 1.0 | 1.0 | 250.0 | 595.0 | 1.0 |
| beta[4] | 1.0 | 0.00013 | 0.0022 | 1.00 | 1.0 | 1.0 | 279.0 | 665.0 | 1.0 |
| beta[5] | 1.0 | 0.00017 | 0.0023 | 1.00 | 1.0 | 1.0 | 180.0 | 427.0 | 1.1 |
| sigma | 2.0 | 0.70000 | 1.1000 | 0.90 | 2.7 | 3.2 | 2.0 | 4.8 | 11.3 |
[9]:
print(mcmc_random_inits_fit.diagnose())
Processing csv files: /tmp/tmpz1qbkg8k/blr-20211119014527_1.csv, /tmp/tmpz1qbkg8k/blr-20211119014527_2.csv, /tmp/tmpz1qbkg8k/blr-20211119014527_3.csv, /tmp/tmpz1qbkg8k/blr-20211119014527_4.csv
Checking sampler transitions treedepth.
Treedepth satisfactory for all transitions.
Checking sampler transitions for divergences.
544 of 4000 (14%) transitions ended with a divergence.
These divergent transitions indicate that HMC is not fully able to explore the posterior distribution.
Try increasing adapt delta closer to 1.
If this doesn't remove all divergences, try to reparameterize the model.
Checking E-BFMI - sampler transitions HMC potential energy.
The E-BFMI, 0.008, is below the nominal threshold of 0.3 which suggests that HMC may have trouble exploring the target distribution.
If possible, try to reparameterize the model.
The following parameters had fewer than 0.001 effective draws per transition:
sigma
Such low values indicate that the effective sample size estimators may be biased high and actual performance may be substantially lower than quoted.
The following parameters had split R-hat greater than 1.1:
beta[5], sigma
Such high values indicate incomplete mixing and biased estimation.
You should consider regularizating your model with additional prior information or a more effective parameterization.
Processing complete.